I Figured Out How to Predict the Stock Market — and Still Lost Money.

I created the holy grail, everything one could wish for — but learned quite an expensive lesson regardless.

Background

To understand what I did, we must first learn some things about how stock prices move. 

Everyone has their own view of how prices move, but a common one — and one that I abide by, is that stock prices can be modeled through something known as Brownian motion. Brownian motion is the observation of random movements from point A to point B. Examples of this are dust floating in a room, or a gas molecule bouncing around randomly. 

When applied to stock prices, this theory says that prices move in a random motion and what happened before has no bearing on what will happen next. Many, including myself, disagree with this, so geometric Brownian motion served as the remedy. The difference between geometric and regular Brownian motion is that geometric motion assumes some drift. This drift represents the expected direction of whatever is being modeled.

We know that the S&P 500 has a positive drift in the long run, so we can make random paths and add a drift so that our prediction can closely model real-world prices. Of course, this builds on the assumption that prior prices have an effect on current/future prices. 

Implementing

With the above in mind, we must now go over how short-term prices will be predicted.

• First, you take the volatility of the time period. If you’re looking at one day, then use the standard deviation of the log returns (I recommend multiplying this number by 10 or more).
• Take that volatility number and add or subtract any random number between 0 and 1. This represents the random nature of prices. (You can use the volatility of the entire time period, or you can weigh the most recent periods higher. In volatile periods, your model will remain accurate because the range will always expand and contract based on changes in recent volatility.)
• Multiply that number by the last price and add it to the last price. This new price represents your predicted price for the next time period.
• Do steps 2–3, 10,000 more times and store each result. 
• Take all of your predicted values and return only the first and third quartiles. This represents your expected range of prices for the next time period. 

Now, how accurate is this anyway? Well, see for yourself:

Using the 50 Day period (taking the past 50 days to predict daily price on the 51st day), our model accurately returned a daily price range 85% of the time, with a 482 sample size and an average range spread of $95 (S&P 500 Index). Message me for the code for this, so that you may replicate this yourself and see that the extraordinarily significant results stretches across all periods, even back to the 1970s!

So now that the model is built and proven to be accurate, let’s make some money. 

Pre-Trade

Since we know what the price range of the next day will be, it should be easy to monetize, right? Well, not very. One way to monetize this in the options market is to sell 1 day to expiration credit spreads around this range. Unfortunately, since the probability of these not paying off is low, the premium you would collect is also very low. So using options, you would get paid about $15, 85% of the time, but 15% of the time, you’ll lose $500. So options are out. 

This leaves Kalshi, the prediction market which allows you to bet on the closing price of the S&P 500. Every day, a market opens that allows you to place bets on where the major indexes will close. However, these bets are quoted in $50 intervals, e.g. 4000–4049.99, 4050–4099.99, etc. But our daily model has an average range of nearly $95, so we’ll have to scale down our time frame to get a smaller range. 

Let’s check how accurate the model is on a 15 minute basis: 

We see that the accuracy is still comparable, topping out at nearly 90% (again, the model is saying, in the next 15 minutes, the price will be within this range, each time that it is, it is counted as a win), and an average spread of just $15. 

With that tight range, we can put on an initial position, and just hedge out risk when the market changes. With all of that said, I decided to throw $500 at this, just for testing. 

The Trade

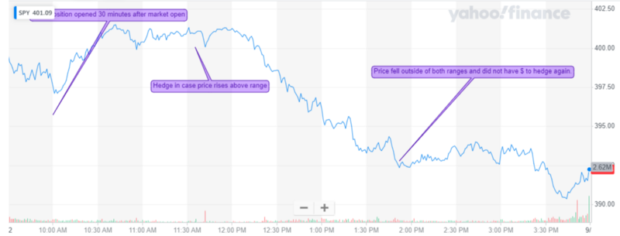
The first three days were a success! My strategy was buying the initial position based on the range the model spit out, and then hedging with the new range if the market had a move.

Things were going well, I was sure that billionaire status was just a thousand trades away, but do you see the risk yet? Just think for a second. 

The risk to this is that the market may move in the direction of your hedge, but it can also move past it and it may even reverse and fall far below both your hedge and initial position. When that happens, you won’t have enough liquid cash to hedge the new range, and then you’ll lose on all of the positions you own, and be wiped out. Which is exactly what happened. 

Final Thoughts

So, there is indeed a way of accurately predicting stock price ranges, but of course, monetizing it is the hard part. If you have any suggestions or ideas on how you can optimize or monetize this, please feel free to comment or implement this yourself and let me know how it goes. 

Normally, I would leave a link to the source code I wrote for this, but I believe that this is too significant to make public. If you have any ideas for your own implementation, just shoot me an inquiry. 

If this whet your appetite and you’d like to read more like it, head on over to The Financial Journal!